Overland flow
Originally LAPSUS was developed to simulate overland flow (either Hortonian or saturation overland flow) erosion and sedimentation in the Mediterranean region of Southern Spain (Schoorl, 2001).
Overland flow (or surface run-off) occurs in two cases:
1. when the intensity of precipitation that reaches the surface exceeds the infiltration capacity of the soil. This process is known as Hortonian overland flow.
2. when the combination of precipitation intensity and duration (and run-on from higher areas) saturates the soil and raises the water table to the surface. This process is known as saturation overland flow.
Case Studies: Netherlands; Belgium; Spain; Kenya; Ghana, Kenya and Mali
See also:
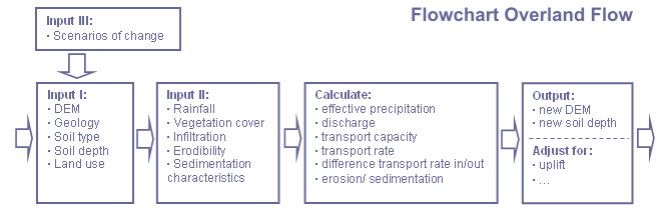
Technical Information
The water erosion and sedimentation module of the model has two fundamental assumptions: 1) the potential energy of surface water flow is the driving force for sediment transport and 2) the difference between sediment input and output of a grid cell is equal to the net increase in storage (continuity equation for sediment movement) (Schoorl et al., 2000). The process description is derived from early works of Kirkby (Kirkby, 1971) and Foster and Meyer (Foster and Meyer, 1972a; Foster and Meyer, 1972b), who use 2D formulas to calculate water erosion and sedimentation. For the LAPSUS model the formulas are adapted to be able to simulate spatial (3D) water erosion and sedimentation (Schoorl et al., 2000). The formulas discussed below are based on the 2D formulas of Kirkby and Foster and Meyer and with the accompanying units (Foster and Meyer, 1972a; Foster and Meyer, 1972b; Kirkby, 1971).
After calculating discharge Q the sediment transport capacity C (m2 time-1) in the grid cell can be calculated as function of discharge and slope following:
(1.1) C = α·Qm·Λn
Whereby Λ is the slope gradient (∂z/∂x) (-) and m (-) and n (-) are constants giving an indication of the system studied: m = 0 and n = 1 suggests soil creep, while m = n = 3 suggests large rivers (Kirkby, 1971). No strict boundaries can be given as the effect of m and n depends on interactions with other model parameters. Dummy variable α is used to correct the units.The sediment transport rate S (m2 time-1) is calculated following the integrated continuity equation for sediment movement (Eq. 1.2 and 1.3). The composition of the used e-power term in the formula depends on the balance between the transport rate of sediment already in transport S0 (m2 time-1) (incoming sediment fluxes of all higher neighbours in the grid cell) and sediment transport capacity C: if S0 < C erosion results, while when S0 > C sedimentation results. When the grid cell is eroded the following formula for sediment transport rate S is used:
(1.2) S = C + (S0 - C)·e -dx·D/C
When sediments are deposited in the grid cell the following formula for sediment transport rate S is used:
(1.3) S = C + (S0 - C)·e -dx·T/C
Whereby the transport rate of sediment S over grid cell size dx (m) is calculated by comparing sediment transport capacity C with transport rate of sediment already in transport S0 (m2 time-1) minus sediment transport capacity C, reduced by an e-power resulting from grid cell size, detachment capacity D or settlement capacity T and sediment transport capacity C.
Detachment capacity D (m time-1), representing how easy sediment is eroded of the surface, is calculated as function of discharge and slope following:
(1.4) D = Kes·Q·Λ
whereby Kes (m-1) is a lumped surface factor indicating erodibility of the surface. Settlement capacity T (m time-1), representing how easy sediment is deposited on the surface, is calculated following:
(1.5) D = Pes·Q·Λ
whereby Pes (m-1) is a surface factor indicating lumped sedimentation characteristics.
By comparing the sediment transport rate S of the grid cell with the sediment already in transport S0 the change in sediment transport rate dS, and thus erosion or sedimentation, can be calculated following:
(1.6) dS = S - S0
dS can be recalculated to erosion or sedimentation in meter by dividing it by the grid length dx (m) and multiplying it by the time step (time). The resulting value is used to correct the digital elevation model and the soil depth map for the following time step.